PROYECCIONES DIÉDRICAS DE LA ESFERA

PROYECCIONES DE LA ESFERA

Representado su centro O por sus proyecciones diédricas las proyecciones de la esfera están definidas por dos circunferencias máximas de radios iguales al radio de la superficie: en proyección horizontal se aprecia la circunferencia horizontal que pasa por el centro O (ecuador) y en proyección vertical otra circunferencia de igual radio (meridiano frontal).

DETERMINACIÓN DE PUNTOS EN LA SUPERFICIE DE LA ESFERA

Para determinar la proyección horizontal de un punto D dado por su proyección vertical trazaremos por el un plano auxiliar horizontal Q, éste generará una sección circular en la esfera de diámetro AB y centro O. La proyección horizontal de D estará sobre la circunferencia sección mencionada en d1 o d2.

Si se tratase de localizar la proyección vertical de un punto de la esfera dado por su proyección horizontal nos auxiliaríamos de un plano frontal. 

SECCIÓN PLANA DE UN PLANO PROYECTANTE EN LA ESFERA

6.1.7 CONO

 CONO RECTO Y DE REVOLUCIÓN CON LA BASE CONTENIDA EN EL PLANO HORIZONTAL DE PROYECCIÓN.

SECCIÓN DE UN CONO POR UN PLANO OBLICUO.

6.1.6 CILINDRO

CILINDRO RECTO Y DE REVOLUCIÓN CON LA BASE CONTENIDA EN EL PLANO HORIZONTAL DE PROYECCIÓN.

Proyecciones de un cilindro de revolución conocida su altura -h- y el radio de su circunferencia generatriz y teniendo una de sus bases contenida en el plano horizontal de proyección, donde su eje es perpendicular a este plano, su generatriz es una circunferencia y su sección recta será por tanto un circulo. 

Dibujamos en proyección horizontal la base de radio dado y en proyección vertical el contorno aparente de las generatrices del cuerpo que no son sino segmentos verticales de proyecciones horizontales a y b y de cota la altura -h- dada. Las bases circulares se muestran en proyección vertical como segmentos horizontales de longitud igual al diámetro de la circunferencia generatriz.

SECCIÓN DE UN CILINDRO POR UN PLANO PROYECTANTE.

SECCIÓN DE UN CILINDRO POR UN PLANO OBLICUO.

PROYECCIONES EXAEDRO

 Hexaedro o cubo con una de sus caras apoyada en el plano horizontal de proyección.

Ejercicios de Hexaedro:

CUBO CON UNA DE SUS CARAS EN UN PLANO OBLICUO

HEXAEDRO APOYADO EN UN PLANO OBLICUO CUALQUIERA

Vídeos explicativos:

CUBO APOYADO EN UN PLANO OBLICUO

control 1.7

 

SECCIONES PLANAS

Para determinar una sección plana necesitamos una superficie reglada desarrollable (poliedros, pirámide, cubo, prisma…) o de revolución (cono, cilindro, esfera) y un plano con el que tenemos que cortar ese cuerpo.

Por eso llamamos SECCIÓN PLANA al polígono de intersección formado por un plano que corta a una superficie geométrica. Una vez determinadas las proyecciones de la sección plana, si no estuvieran paralelas a algún plano de proyección, procederemos a calcular su verdadera magnitud, por abatimiento.

SECCIÓN PLANA PRODUCIDA POR UN PLANO PERPENDICULAR A UN PLANO DE PROYECCIÓN

La intersección producida en una superficie geométrica por un PLANO PERPENDICULAR A UN PLANO DE PROYECCIÓN, determina la sección plana de forma directa sobre la proyección del cuerpo geométrico en donde la traza del plano se muestra perpendicular. 

SECCIÓN PLANA PRODUCIDA POR UN PLANO HORIZONTAL.

SECCIÓN PLANA PRODUCIDA POR UN PLANO DE PERFIL

SECCIÓN PLANA PRODUCIDA POR UN PLANO PROYECTANTE

SECCIÓN PLANA PRODUCIDA POR UN PLANO PARALELO A L.T.

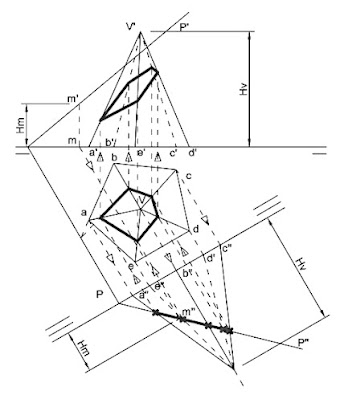
SECCIÓN PLANA PRODUCIDA POR UN PLANO OBLICUO

En el caso de que la intersección sea por un plano oblicuo, los puntos de intersección no se determinan directamente, la forma de resolver la sección plana consistiría en convertirlo en Plano Proyectante mediante cambio de plano.

SECCIÓN PLANA Y VERDADERA MAGNITUD

La intersección producida en una superficie geométrica producirá la SECCIÓN PLANA, de la que se necesitará determinar su VERDADERA MAGNITUD. Para ello, en el caso de intersección con un plano oblicuo, lo más fácil será abatir el plano proyectante resultante del cambio de plano.

IMPORTANTE: Tanto las proyecciones de la sección plana como su verdadera magnitud se dibujarán en linea gruesa contornos, diferenciando partes vistas y ocultas y se rayaran con lineas finas paralelas equidistantes (1.5/2 mm) e inclinadas aprox. 45º sobre alguno de los ejes principales del dibujo, sin quedar paralelas a ninguno de los lados de la forma, y con distinta orientación tanto en proyecciones como en su abatimiento.

Resumen de las Orientaciones DT II (PEvAU): DIÉDRICO

Comentario resumen de las Directrices y Orientaciones Generales de Dibujo Técnico II para la Prueba de Evaluación y Admisión a la Universidad (PEvAU): Orientaciones Curso 2020/21.

BLOQUE II: SISTEMAS DE REPRESENTACIÓN

DIÉDRICO

Se hará hincapié en las siguientes cuestiones:

• Determinar ángulos entre rectas, de rectas con planos y de rectas y planos con los de proyección.
• Determinar una recta conociendo el ángulo que forma con uno de los planos de proyección.
• Determinar un plano conociendo el ángulo que forma con uno de los planos de proyección. 
• Cuerpos: - Situar puntos sobre su superficie. - Intersección con rectas. - Secciones producidas por planos cualesquiera.
• Cuando no se indique expresamente se podrá utilizar libremente el abatimiento, giro o cambio de plano de proyección.
• El tetraedro y el cubo siempre tendrán una cara apoyada sobre cualquier tipo de plano.
• El octaedro sólo se pedirá con su diagonal perpendicular a un plano de proyección.
• Los prismas y pirámides siempre serán regulares.
• Los cilindros y conos siempre serán de revolución. 
• Cuando la solución de un apartado/ejercicio sean las proyecciones de rectas, trazas de planos, cuerpos, secciones, etc., es implícito que el alumnado aplique vistos y ocultos.

Los ejercicios, a los efectos de la PEvAU, no propondrán:

• Determinar la mínima distancia entre dos rectas que se cruzan. 
• Determinar una recta oblicua conocidos los dos ángulos que forma con los planos de proyección.
• Determinar un plano oblicuo conocidos los dos ángulos que forma con los planos de proyección.