Control 1.5 (DT II)

Control 2 (DT I)

Paralelismo en diédrico

Dos elementos son paralelos cuando nunca se cortan y, por tanto, no contienen ningún punto en común.

En el caso del lenguaje diédrico esta circunstancia se manifiesta directamente en los caso de paralelismo entre rectas y entre planos, de manera qué decimos que son paralelos si sus proyecciones o trazas homónimas lo son.

Sin embargo, en el caso de paralelismo entre recta y plano, sólo podemos comprobar que una recta es paralela a un plano, si lo es, al menos, a una de las infinitas rectas contenidas en dicho plano.

Conclusiones:

Como se puede comprobar la relación geométrica en el espacio que llamamos paralelismo en Sistema Diédrico se resuelve de manera muy sencilla. Teniendo los siguientes prnicipios:

• El paralelismo entre rectas se observa directamente en proyecciones.
• El paralelismo entre planos también se ve directamente en proyecciones.
• El paralelismo entre recta y plano necesita siempre de una recta auxiliar de comprobación.
• Y sería excepciones a todo esto, las rectas de perfil y los planos paralelos o que pasen por LT que necesitarán la vista de perfil.

Control 1.4 (DT II)

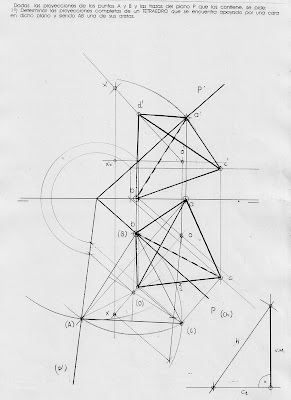
PROYECCIONES DIÉDRICAS DEL TETRAEDRO

Tetraedro con una de sus caras apoyada en el plano horizontal de proyección:

Tetraedro con una de sus aristas contenida en plano horizontal de proyección en equilibrio:

Tetraedro con una de sus caras apoyada en un plano oblicuo:

Control1.3 (DT II)

SUPERFICIES GEOMÉTRICAS

Un punto al desplazarse produce una línea (generatriz) que siguiendo un determinado sentido geométrico (directriz) genera una superficie.

Las superficies geométricas no tienen volumen propio,  son simplemente un límite espacial (plano geométrico).

Por su naturaleza las superficies, se clasifican en :

SUPERFICIES REGLADAS, cuando la generatriz es una línea recta. Que son desarrollables, cuando puede desplegarse sobre un plano sin experimentar rotura ni deformación. O, alabeadas, si no se pueden desarrollar en el plano.

SUPERFICIES CURVAS, cuando la generatriz es una línea curva. La más importantes es la esfera (de 2º grason las de revolución generadas por una curva que gira alrededor de una recta fija denominada eje y contenida en su plano.



SUPERFICIES REGLADAS

Dentro de las superficies regladas podemos distinguir: 

Superficies poliédricas: que están formadas por varias caras planas, que si son todas iguales se denominan superficies poliédricas regulares y el cuerpo al que envuelven, poliedro regular.

Son cinco los POLIEDROS regulares, a saber:

TETRAEDRO: Tiene cuatro caras, estas son triángulos equiláteros.

HEXAEDRO: Tiene seis caras, son cuadrados.

OCTAEDRO: Tiene ocho caras, son triángulos equiláteros.

DODECAEDRO: Formado por doce caras pentagonales.

ICOSAEDRO: Formado por veinte caras que son triángulos equiláteros.

Superficies radiadas: superficies que se obtienen por el desplazamiento de una linea recta alrededor de un eje y siguiendo una determinada directriz, bien poligonal o curva.

CILÍNDRICAS cuando la recta generatriz se mantiene paralela al eje; siendo de revolución cuando la directriz es una circunferencia y prismática si es un polígono, como el CILINDRO o el PRISMA.

CÓNICAS cuando la recta generatriz se corta en un punto del eje; siendo de revolución cuando la directriz es una circunferencia y prismática si es un polígono, como el CONO o la PIRÁMIDE.

SUPERFICIES CURVAS

En las superficies curvas destacamos la ESFERA, cuando su generatriz es una circunferencia que gira sobre uno de sus diámetros.

La superficie tórica o TORO, se obtiene si es una circunferencia la que gira sobre un eje describiendo un movimiento circular.

Y la ESCOCIA se engrendra por dos o más arcos tangentes entre sí, que giran aldededor de un eje

SISTEMA DIÉDRICO. Intersección de planos.

MÉTODO GENERAL EN LA INTERSECCIÓN DE PLANOS.

La intersección de dos planos genera una recta. El método general para calcular la intersección entre dos planos, consiste en dibujar las rectas intersección de estos planos  con otros dos auxiliares. De manera que uniendo  los puntos de intersección de las rectas intersección obtenidos entre los planos, tomados tres a tres, obtenemos la recta intersección buscada.

INTERSECCIÓN DE PLANOS OBLICUOS.

Los planos auxiliares en diédrico, por regla general, son  los propios planos de proyección, lo que nos lleva a una solución directa: la recta de intersección de dos planos tiene sus trazas en la intersección de las trazas de los planos.

CASOS PARTICULARES DE INTERSECCIÓN DE PLANOS:

Intersección de plano oblicuo con un  plano paralelo a un plano de proyección.

Intersección de plano oblicuo con plano proyectante.

Intersección de planos proyectantes horizontal y vertical entre sí.

Intersección de proyectantes del mismo tipo entre sí.

Intersección de un plano oblicuo con uno paralelo a LT.

Intersección de planos paralelos a LT.

INTERSECCIÓN DE PLANOS CUANDO SUS TRAZAS SE CORTAN FUERA DE LOS LÍMITES DEL DIBUJO.

Al no poder utilizar la intersección de trazas, dibujaremos planos auxiliares, que nos darán en su intersección con los planos dados puntos de la recta de intersección buscada.

SISTEMA DIÉDRICO: Alfabeto del plano

La distintas posiciones que puede ocupar el plano en el sistema diédrico da lugar a su clasificación como ALFABETO DEL PLANO, un total de 24 posiciones que se resumen en las siguientes: 

Plano oblicuo a los planos de proyección

Los que no son paralelos ni perpendiculares a los planos de proyección. Presentan sus trazas oblicuas respecto de la línea de tierra.

Planos proyectantes

Son perpendiculares a uno de los planos de proyección y oblicuos al otro, se utilizan frecuentemente como planos auxiliares. Hay dos tipos: Proyectante Vertical y Proyectante Horizontal.

Planos paralelos a los planos de proyección.

Son paralelos a alguno de los planos de proyección, tiene sólo una traza paralela a LT y los hay de dos tipos: Paralelos al PV y Paralelos al PH.

Planos paralelos a la línea de tierra.

Presentan sus trazas vertical y horizontal paralelas a la línea de tierra, pero siempre que no sean equidistantes a ella, porque entonces se convertirían en Paralelos a los Planos Bisectores.

Planos que pasan por LT.

Su intersección con los planos de proyección está en línea de tierra por lo que sus trazas no son representativas. Se representa de forma normalizada y la indicación de las proyecciones de uno de sus puntos y dibujando dos trazos por debajo de la línea de tierra; se puede apreciar mejor si se ve y representa de perfil.

Planos perpendiculares a los planos bisectores.

Son planos oblicuos a los plano de proyección pero que debido a su posición particular, además se colocan como perpendiculares a los Planos Bisectores, circunstancia que se advierte por dibujar ángulos iguales respecto a LT. Los hay de dos tipos: Perpendicular a B1 y Perpendicular a B2.

Plano de Perfil.

Es perpendicular al plano vertical y horizontal de proyección. Sus trazas se presentan perpendiculares a la línea de tierra. Las proyecciones de los elementos en él contenido, coinciden con sus trazas por lo que, y con objeto de obtener una proyección más representativa de sus elementos, abatimos este plano sobre el vertical de proyección presentándose de este modo en verdadera magnitud y forma (Plano de perfil como plano auxiliar de proyección)