La HOMOTECIA es una transformación geométrica en el plano, en la cual los puntos relacionados o transformados, que se denominan homólogos u homotéticos, cumplen las siguientes condiciones:
- Los puntos homotéticos están alineados con un tercero fijo llamado centro de la Homotecia (O).
- La relación entre los segmentos definidos por este centro y los puntos transformado y original es una constante denominada razón de la homotecia (k).
Propiedades:
Rectas homotéticas siempre son paralelas, y proporcionales a la razón de la homotecia (k) y ángulos homotéticos son iguales.
Dos figuras homotéticas guardan relación de SEMEJANZA.
Casos:
- Si la constante k es mayor que 0, la Homotecia se denomina directa o positiva, y en ella los puntos homotéticos están al mismo lado del centro.
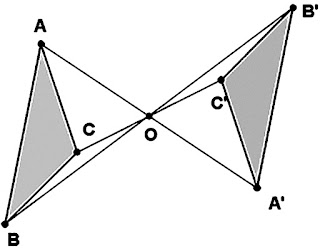
- Si la constante k es menor que 0, se denomina inversa o negativa, y en ella los puntos homotéticos están en lados diferentes con respecto al centro .
- Si la constante k es 1, la figura homotética coincide con la original, y la transformación se denomina identidad.
- Si la constante k es -1, la Homotecia se convierte en una Simetría Central
Resumiendo:
- Si el valor absoluto de la constante k es mayor que 1, la Homotecia produce un aumento de tamaño (la figura final es mayor que la original).
- Si el valor absoluto de la constante k es menor que 1, la Homotecia produce una disminución de tamaño (la figura final es menor que la original).
Si pinchas en la imagen
accederás a una demostración en GeoGebra
Homotecia de la circunferencia:
La homotética de una circunferencia es otra circunferencia cuyos centros también lo son, y cuyos puntos son homotéticos uno a uno.
Dadas dos circunferencias cualesquiera, siempre existen dos Homotecias que las relacionan, una de ellas directa y otra inversa. En cualquiera de los dos casos, el centro de la Homotecia está alineado con los dos centros de las circunferencias (en las figuras se muestran las homotecias directa e inversa que relacionan dos circunferencias).









No hay comentarios:
Publicar un comentario