PELOTAZO 1

 

control 1.6

 

control 1.5

 

control 1.4

 

control 1.2

 

ÍNDICE DE CONTENIDOS

1.- SISTEMAS DE REPRESENTACIÓN
1.1. Proyecciones

1.2. Fundamentos de los sistemas de representación

2.- SISTEMA DIÉDRICO ( I ), PUNTO, RECTA Y PLANO
2.1. Alfabeto del punto
2.2. Alfabeto de la recta
2.3. Alfabeto del plano

3.- SISTEMA DIÉDRICO ( II ), PERTENENCIAS E INTERSECCIONES
3.1. Pertenencias y determinaciones
3.2. Intersecciones de planos
3.3. Intersección de recta y plano

4.- SISTEMA DIÉDRICO ( III ), PARALELISMO Y PERPENDICULARIDAD
4.1. Paralelismo: rectas y planos
4.2. Perpendicularidad: rectas y planos

5.- SISTEMA DIÉDRICO ( IV ), VERDADERAS MAGNITUDES
5.1. Abatimientos
5.2. Giros
5.3. Cambios de plano

6.- SISTEMA DIÉDRICO ( V ), SUPERFICIES
6.1. Representación diédrica de superficies regladas desarrollables y de revolución más usuales
6.2. Secciones planas

7.- SISTEMA DIÉDRICO ( VI ), PRÁCTICAS
7.1. Prácticas de aplicación del Sistema Diédrico

8.- NORMALIZACIÓN ( I )
8.1. La Norma en el dibujo técnico
8.2. Formatos y líneas

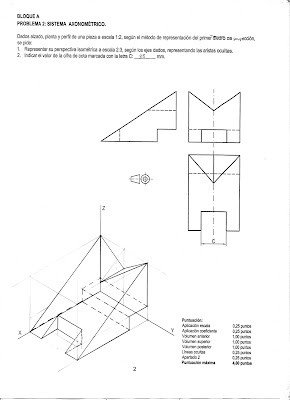
9.- SISTEMA AXONOMÉTRICO
9.1. Fundamentos
9.2. Escalas axonométricas y coeficientes de reducción
9.3. Representaciones isométricas
9.4. Axonometría oblicua, ángulos de fuga y coeficientes de reducción
9.5. Representación de cuerpos en caballera

10.- PRACTICAS DE PERSPECTIVA
10.1. Isométrica
10.2. Caballera
10.3. Cónica

11.- NORMALIZACIÓN ( II ), CONVENCIONALISMOS GRÁFICOS
11.1. Secciones y cortes
11.2. Empleo de roturas

12.- NORMALIZACIÓN ( III ), ACOTACIÓN
12.1. Elementos de acotación
12.2. Normas y sistemas de acotación

13.- TRAZADO Y CROQUIZADO
13.1. Prácticas de trazado
13.2. Ejercicios de croquizado

14.- TEORÍA DE LAS CONSTRUCCIONES GRÁFICAS FUNDAMENTALES
14.1. Lugares geométricos
14.2. Triángulos
14.3. Cuadriláteros
14.4. La circunferencia

15.- PROPORCIONALIDAD Y CONSTRUCCIÓN DE ESCALAS
15.1. Teorema de Thales
15.2. Media, tercera y cuarta proporcional
15.3. Construcción y utilización de escalas

16.- CONSTRUCCIÓN RAZONADA DE FORMAS POLIGONALES REGULARES
16.1. Construcción de polígonos inscribibles en circunferencias
16.2. Construcción de polígonos conociendo el lado
16.3. Polígonos estrellados

17.- FIGURAS PLANAS EQUIVALENTES
17.1. Equivalencia
17.2. Determinación gráfica de equivalencias

18.- TRANSFORMACIONES GEOMÉTRICAS
18.1. Transformaciones en el plano
18.2. Homotecia
18.3. Homología
18.4. Afinidad
18.5. Inversión

19.- POTENCIA Y POLARIDAD
19.1. Potencia y polaridad
19.2. Eje y centro radical

20.- ANÁLISIS Y TRAZADO DE CURVAS PLANAS
20.1. Curvas cónicas
20.2. Curvas técnicas
20.3. Curvas compuestas

21.- ESTUDIO SISTEMÁTICO DE TANGENCIAS
21.1. Determinación de tangencias

22.- ARTE Y DIBUJO TÉCNICO
22.1. La geometría en el arte
22.2. Estética y dibujo técnico.

RESULTADO PEVAU 2023

El estudio estadístico de la media de los resultados de Selectividad de 2009-2013, arroja que la media obtenida en las pruebas de Dibujo Técnico sería de 7,32 ptos. (4ª mejor nota del centro).

En 2019, la nota media de DT del IES Aguilar y Eslava fue de 9´05 ptos. frente a la de la Universidad de 5´96.

Más de 3 puntos de diferencia (2º mejor nota del centro).

En 2021, después de dos cursos de pandemia y las circunstancias sanitarias sufridas (baja profesor...), la nota media del IES Aguilar y Eslava cayó hasta un 5 , siendo la de la Universidad  de 5´6 ptos. 

Una diferencia de -0´6 puntos (16º nota del centro).

En 2022, recuperada la "normalidad" los resultados de la PEvAU en nuestro centro vuelven a ser muy positivos, casi medio punto por encima de la media de Córdoba y Andalucía.

Y en el caso de DIBUJO TÉCNICO (7´82 ptos.), casi PUNTO Y MEDIO por encima de la media (5º nota mejor del centro).

En 2023, sigue el modelo de pandemia (opcionalidad total) los resultados de la PEvAU en nuestro centro siguen siendo positivos, más de medio punto por encima de la media de Córdoba y Andalucía.

Y en el caso de DIBUJO TÉCNICO (7´92 ptos.), casi  MEDIO PUNTO por encima de la media (entre las mejores seis notas del centro). Destacando: 3 (10), 2 (+9) y 3 (+8), es decir 67% alumnado consigue buena nota.

PRESENTACIÓN CURSO 2023-2024

Este curso de DIBUJO TÉCNICO (II) nos proporcionará los conceptos, conocimientos y destrezas propias de una materia fundamental en el campo de las Ciencias e Ingenierías, mediante la introducción en los sistemas y técnicas de representación gráfica y su adecuada aplicación, con vista a la consecución de dos objetivos generales:

Superar las pruebas de acceso a la universidad (PEvAU) con buena nota.

Acceder con garantías a posteriores estudios universitarios o profesionales.

PROGRAMACIÓN

La programación de la asignatura de Dibujo Técnico para el curso 2023-2024, se ajusta al Decreto  327/2010,  de  3  de  julio,  por  el que  se aprueba  el  Reglamento  Orgánico  de  los  Institutos  de  Educación  Secundaria  en Andalucía  que en su  artículo  29, en  el punto 1, determina que:  “Las programaciones didácticas  son instrumentos  específicos  de  planificación,  desarrollo  y  evaluación  de cada materia, módulo o, en su caso, ámbito del currículo establecido por la normativa vigente." Pero obviamente, teniendo en cuenta la vigencia o prorroga de la PEVAU, seguiremos teniendo presente la Orden de 15 de enero de 2021, por la que se desarrollaba el currículo correspondiente a la etapa de Bachillerato en la Comunidad Autónoma de Andalucía. 

Los saberes básicos de esta materia se organizan en torno a tres bloques fundamentales e interrelacionados, ligados a su vez a las competencias específicas: 

- En el bloque “Geometría Plana” el alumnado abordará la resolución de problemas sobre el plano e identifica su aparición y su utilidad en diferentes contextos. También se plantea la relación del dibujo técnico y las matemáticas y la presencia de la geometría en las formas de la arquitectura e ingeniería.  

- En el bloque “Geometría Descriptiva” se pretende que el alumnado adquiera los saberes necesarios para representar gráficamente la realidad espacial, con el fin de expresar con precisión las soluciones a un problema constructivo o de interpretarlas para su ejecución. 

- Y en el bloque “Normalización y documentación gráfica de proyectos” se dotará al alumnado de los saberes necesarios para visualizar y comunicar la forma y dimensiones de los objetos de forma inequívoca siguiendo las Normas, con el fin de elaborar y presentar, de forma individual o en grupo, proyectos sencillos de ingeniería o arquitectura.

ORIENTACIONES DIDÁCTICAS Y METODOLÓGICAS

La metodología empleada facilitará un aprendizaje competencial. Los procesos de aprendizaje del dibujo técnico deben girar principalmente en torno a actividades de carácter práctico. Debe favorecer la capacidad para aplicar los métodos de investigación propios de la materia y aprender tanto de forma autónoma y como de forma colaborativa. Esta manera de organizar el proceso de enseñanza, en torno a actividades que promuevan el aprendizaje directo del alumnado, supone una estrategia metodológica que facilita la aplicación de los conocimientos, destrezas y actitudes a la realidad más cercana al alumnado. El objetivo debe ser que los aprendizajes sean permanentes, significativos y transferibles.

Es importante que el alumnado comprenda la aplicabilidad práctica de la materia, por ello, se establecerá una organización de los contenidos de forma globalizada. Es conveniente dar un significado a todos conceptos mediante una presentación progresiva, estableciendo conexiones entre los conocimientos adquiridos en todos los saberes básico para que el aprendizaje sea significativo. Para potenciar la aplicabilidad práctica de la asignatura es importante plantear situaciones contextualizadas, donde el uso de los contenidos teóricos sirva para la resolución de problemas, requiera actividad y despierten el interés de los y las estudiantes.  

El carácter instrumental del dibujo técnico permite trabajar de forma interdisciplinar contenidos comunes con otras materias, especialmente del ámbito artístico, tecnológico, físico y matemático, además de procurar la orientación del alumnado hacia campos del conocimiento o estudios superiores relacionados.  

SITUACIONES DE APRENDIZAJE.

Las situaciones de aprendizaje en el proceso de formación en la etapa de bachillerato deben contemplar tareas que estimulen la asunción de una postura autónoma, crítica, comprometida con la calidad del desempeño, que oriente la actuación del estudiante en la solución de problemas a partir de la integración de sus recursos cognitivos y motivacionales expresados en la conducta de manera coherente, con eficiencia, autocrítica, flexibilidad y perseverancia. 

El diseño de situaciones de aprendizaje debe propiciar la construcción por parte del estudiante de competencias clave y específicas necesarias para un desempeño eficiente, ético y responsable de la materia. El conocimiento es sólido y útil si el alumnado adquiere los conocimientos y es capaz de aplicarlos. Si estos se ponen en práctica de forma activa, la asimilación es cada vez más rica e implica la comprensión del mundo y de dicho conocimiento. Los contenidos desarrollados en cada bloque deben exponerse de manera ordenada ejemplarizándolo con ejercicios resueltos representativos para facilitar su comprensión. 

Se plantearán actividades que se puedan resolver con los contenidos planteados para fundamentar y trabajar lo aprendido.  Las situaciones de aprendizaje diseñadas en la materia de Dibujo Técnico deben estar contextualizadas en realidades profesionales cercanas al alumnado, como puede ser el mundo del diseño, la arquitectura o la ingeniería. Mediante la aplicación práctica pueden poner en juego un conjunto amplio de conocimientos, habilidades o destrezas y actitudes personales.  Los planteamientos de actividades y tareas deben tener en cuenta los distintos ritmos y estilos de aprendizaje mediante prácticas de trabajo individual y colaborativo, graduando los contenidos y la complejidad, desde el trazado de formas planas a las representaciones tridimensionales. 

PROCEDIMIENTOS DE EVALUACIÓN.

Se debe entender el aprendizaje como un proceso continuo. Por ello se realizará una evaluación de forma globalizada, continua y formativa, teniendo en cuenta el grado de desarrollo de las competencias específicas, competencias clave y el progreso en el conjunto de los procesos de aprendizaje. La formación de competencias en la materia de Dibujo Técnico debe lograr de manera simultánea la formación de competencias clave y específicas. No se trata de una adición o sumatoria de competencias sino de su necesaria integración para la consecución del perfil de salida. 

Los indicadores a evaluar atenderán a los siguientes criterios mínimos:

1. Dominio de conceptos y propiedades referidos a la geometría plana. 

2. Conocimiento y práctica en la representación en sistema diédrico. 

3. Representar piezas industriales en perspectiva. 

4. Utilizar correctamente las normas establecidas en el trazado de dibujo técnico. 

5. Regularidad en la entrega de actividades propuestas. 

Se valorará el nivel alcanzado con relación a los saberes básicos, a través de ejercicios y pruebas regulares. Y se establecerán criterios de recuperación adaptados al ritmo de aprendizaje del estudiante, pero sobre los niveles mínimos exigidos. Estos procedimientos para la evaluación de conceptos, destrezas y actitudes, están sustentados en criterios comunes y se basaran en la observación del trabajo desarrollado en clase (actitudes y respeto a la normas de convivencia), corrección de ejercicios prácticos y superación de pruebas de control. 

TRABAJO EN CLASE Y EN CASA.

La materia de Dibujo Técnico necesita, por parte del alumnado, la elaboración de unos apuntes diarios, en su realización y control el profesor valorará la adquisición de conceptos y competencias básicas.

Estos apuntes se completan con el blog de la asignatura y el aula virtual Modle/Classroom que facilitan al alumnado el repaso, la práctica y, también, la autoformación. Además, se valorará complementariamente las respuestas razonadas a las preguntas que se sucedan en las explicaciones de clase. Expresión correcta de ideas y conceptos.

Trabajo en clase 

Se valorará las actitudes y el respeto a las normas de convivencia, que se hará en función de: 

• Faltas injustificadas. 

• Trae el material necesario para la prácticas y para el desarrollo de los contenidos y elaboración de apuntes. 

• Trabaja en clase, responde adecuadamente a las preguntas de clase, atiende, no se distrae... 

• Es puntual en la entrega de ejercicios. 

• Implicación y colaboración con los compañeros. 

• Respeto a las normas de convivencia. 

Ejercicios prácticos de dibujo técnico. 

Relacionados con los saberes básicos de la materia se desarrollarán como láminas (formato DIN A4). Estás prácticas serán realizadas en clase y/o en casa, y son corregidas en primera instancia una vez entregadas, teniéndose en cuenta: corrección en las soluciones, limpieza y trazado, y puntualidad en la entrega. Al finalizar el trimestre se entregarán los ejercicios realizados diariamente presentados adecuadamente en forma de carpeta de ejercicios. 

Pruebas de control. 

Con periodicidad semanal se realizarán pruebas de control (exámenes) que se ajustarán a la notación, características y exigencias equiparables a las pruebas de Acceso a la Universidad. Sus contenidos irán en relación al nivel y competencias de los saberes básicos desarrollados. 

CRITERIOS E INSTRUMENTOS PARA LA EVALUACIÓN.

En los ejercicios y pruebas se valorarán según criterios específicos, sobre todo en lo referente a: 

a) La resolución correcta del problema o exposición concreta del concepto que se plasme. 

b) Presentación, limpieza y pulcritud. 

c) Idoneidad de recursos. 

d) Puntualidad en la presentación de las mismas. 

El alumnado deberá realizar cuantos trabajos y pruebas se planteen en el desarrollo de la clase y dichas actividades, quedarán recogidas en una ficha de seguimiento de carácter individual del alumnado. 

CRITERIOS DE EVALUACIÓN

Siguiendo un sistema de evaluación continua a lo largo del curso los criterios de evaluación se poderarán de la siguiente forma.

1. Resolver problemas de tangencias mediante la aplicación de las propiedades del arco capaz, de los ejes y centros radicales y/o de la transformación de circunferencias y rectas, indicando gráficamente la construcción auxiliar utilizada, los puntos de enlace y la relación entre sus elementos. (10%)
2. Dibujar cónicas, identificando sus elementos principales y utilizando sus propiedades para resolver problemas de pertenencia, tangencia o incidencia (15%)
3. Relacionar  las transformaciones homológicas con sus aplicaciones a la geometría plana y a los sistemas de representación, valorando la rapidez y exactitud en el trazado.(15%)
4. Valorar la importancia de la elaboración de dibujos a mano alzada para desarrollar la "visión espacial", posición relativas de elementos en el espacio, sistema de representación más adecuado, y estrategias de solución de problemas (5%).
5. Representar superficies geométricas tridimensionales en diédrico en posiciones singulares, intersecciones con rectas y planos y sus verdaderas magnitudes (25%).
6. Dibujar axonometrías de superficies geométricas tridimensionales en posiciones singulares, cálculo de coeficientes de reducción, intersecciones con rectas y planos y sus verdaderas magnitudes (20%).
7. Elaborar croquis y planos de proyectos sencillos de diseño, valorando exactitud, rapidez y limpieza (5%). 
8. Presentación de proyectos sencillos de diseño valorando exactitud, rapidez y limpieza (5%).

INSTRUMENTOS DE CALIFICACIÓN. 

La calificación de la EVALUACIÓN tendrá en cuenta: 

• TRABAJO EN CLASE : MÁX. 1 PUNTO.
• EJERCICIOS PRÁCTICOS -Ejercicios realizados en clase y en casa: MÁX. 2 PUNTOS.
• PRUEBAS DE CONTROL : MÁX. 7 PUNTOS.

SISTEMA DE RECUPERACIÓN Y MEJORA. 

Ejercicios prácticos: Si se suspenden, se repiten ejercicios y se presentan al final de trimestre o dentro del plazo establecido 

Recuperación de Pruebas de CONTROL (Exámenes): Para considerar aprobado un examen debe alcanzar la puntuación mínima de 5 (de 0 a 10). La nota final de evaluación se realizará teniendo en cuenta (media) todas las calificaciones de las pruebas realizadas. 

Para poder considerar que el alumno ha aprobado un trimestre debería tener aptos los bloques correspondientes a CONCEPTOS (exámenes) y PROCEDIMIENTOS (ejercicios). Si alguno de los bloques no es apto después de las recuperaciones, el trimestre se puede considerar “no aprobado” . 

Evaluación final: al final del curso se aplicará MEDIA PONDERADA entre los tres trimestres aprobados. Para poder aplicar la media deben estar superados los saberes básicos. También se contempla un sistema de consolidación y subida de nota con pruebas específicas (exámenes opcionales/ simulacro selectividad) como sistema de mejora del rendimiento académico.

CONTROL 3.5

 

CONTROL 3.3 y 3.4

 

CONTROL 3.2

 

Plano Tangente a una Esfera por un Punto de ella

Trazar el plano tangente a una esfera de centro O por un punto A de ella, consiste en  dibujar  el radio que une OA, y  por A ,considerado punto de tangencia, trazar un plano perpendicular apoyándonos en una recta horizontal perpendicular al radio...

Plano Tangente a una Esfera por un Punto de ella (MONGGE)

Cómo acotar una pieza

Manual básico de acotación que incluye las reglas fundamentales para acotar correctamente cualquier pieza, edificio u objeto. 

En este vídeo se repasan las normas fundamentales para acotar:

0.- Introducción (0:00)

1.- Evitar alinear cotas con pieza y ejes (1:33)

2.- Distancia adecuada entre cotas (2:09)

3.- Prolongar líneas auxiliares de cota (2:44)

4.- Tipos de extremos de líneas de cota (3:14)

5.- Cotas pequeñas (4:29)

6.- Evitar cruces de cotas (5:28)

7.- Las líneas auxiliares de una cota deben comenzar en la misma vista (6:03)

8.- Tamaño de cifras (6:50)

9.- Número de cotas adecuado (7:38)

10.- Repartir cotas entre las vistas (8:29)

11.- Posición de las cifras de cota (8:57)

12.- Disposición de las cotas (10:36)

13.- Acotar diámetros (12:04)

14.- Acotar radios (14:29)

15.- Acotar esferas (15:47)

16.- Líneas de cota incompletas (16:56)

17.- Acotar elementos iguales (18:04)

https://www.arturogeometria.com/

Resolución de tangencias

DIRECTRICES Y ORIENTACIONES GENERALES PARA LAS PRUEBAS DE ACCESO Y ADMISIÓN A LA UNIVERSIDAD

Problemas de tangencias aplicando las propiedades de los ejes y centros radicales, indicando gráficamente la construcción auxiliar utilizada, los puntos de enlace y la relación entre sus elementos.

1. Circunferencia tangente a otras dos dado el punto de tangencia sobre una de ellas. (Geogebra)

https://www.slideshare.net/naonito/circunferencias-tangentes-a-otras-dos-dado-el-punto-de-tangencia-en-una-de-ellaspor-potencia

Las circunferencias solución deberán tener la misma potencia que las dadas respecto de un centro radical, que debe permanecer, forzosamente, al eje radical de las dadas. Puesto que las soluciones deben ser tangentes a la circunferencia con el punto de tangencia dado, el eje radical correspondiente a dichas soluciones será además tangente en ese punto de tangencia. En la intersección de ambos lugares se encontrará el centro radical, a partir del cual será sencillo determinar los puntos de tangencia.

2. Trazar las circunferencias tangentes a una recta, que pasen por dos puntos. Geogebra

Los centros solución han de estar sobre la mediatriz de los puntos dados.

Hallaremos un punto P en r, que pertenece al eje radical de las soluciones.  P tiene la misma potencia respecto de una circunferencia cualquiera auxiliar que pasa por AB, que respecto de las soluciones.

3. Circunferencias tangentes a dos rectas y que pasen por un punto (Geogebra)

Los centros estarán situados sobre la bisectriz.

Determinamos un punto P´simétrico de P respecto a la bisectriz. De esta forma se resuelve el problema reduciéndolo al caso anterior.

Este problema también se puede resolver por homotecia o inversión (Mongge):

4. Circunferencias tangentes a un circunferencia dada y que pasan por dos puntos:

En este caso, los puntos podrán ser interiores o exteriores a la circunferencia dada. Veamos el caso cuando los puntos son exteriores:

Ver en Geogebra

A continuación, el caso cuando los puntos son interiores.

Por AB, pasa el eje radical de las circunferencias solución. Y en la mediatriz estarán sus centros. Bastará dibujar una circunferencia auxiliar secante con la dada para determinar el eje radical que comparte la dada con las soluciones. Donde se corten ambos ejes, se determinará un punto que tenga la misma potencia respecto de la dada y las soluciones.

5. Circunferencias tangentes a otra y a una recta, dado el punto de tangencia sobre la recta.

Utilizando una circunferencia auxiliar tangente a r en T, y secante a la circunferencia dada, se determina un punto en r que tiene la misma potencia  respecto de la circunferencia dada que las soluciones. Los centros buscados están en la perpendicular a r que pasa por T.

6. Circunferencia tangente a otra en un punto de ella y a una recta dada.

La recta tangente a la circunferencia por el punto dado es el eje radical que pertenece a las soluciones buscadas y a la dada. Donde corte este eje a r será el centro radical de las tres circunferencias. Por tanto tiene la misma potencia de P a T que las los puntos de tangencia de las soluciones en r.

7. Circunferencias tangentes a otra y a dos rectas

Este problema se resuelve por dilataciones, reduciendo el problema al caso anterior nº 2. Las dilataciones deben emplearse adecuadamente para conseguir todos los resultados posibles. Hay que ampliar y reducir para obtener las circunferencias solución tangentes interiores y exteriores a la dada.

8. Circunferencias con centros sobre una recta r que pasan por un punto de ella y son tangentes a otra circunferencia dada.

Las tangentes común a las soluciones es una recta que pasa por P y es perpendicular a r (eje radical). Para determinar el centro radical se dibuja una circunferencia auxiliar con centro en r que pase por P y secante a la dada. 

9. Circunferencias con centro sobre una recta que pasan por un punto dado y son tangentes a otra circunferencia dada.

Por el simétrico de P respecto a r pasarán las circunferencias solución. Por lo que, de esta manera, se reduce el problema al caso nº 4: circunferencias que pasan por dos puntos y son tangentes a otra dada. 

10. Circunferencias con centros en una recta, tangentes a otras dos dadas.

Se resolverá aplicando lo dicho en el párrafo anterior y utilizando las dilataciones convenientes para reducir una de las dos circunferencias a un punto. Se deben tener en cuenta las soluciones tangentes interiores y exteriores.

Pelotazo 2ªEvaluación

 

Construcción razonadas de POLÍGONOS REGULARES

TRAZADO DE POLÍGONOS REGULARES CONOCIENDO LA CIRCUNFERENCIA CIRCUNSCRITA

 -Procedimiento general-

Para ello nos apoyamos en la división de dicha circunferencia en un número partes iguales.

Este procedimiento se utilizará solo cuando el polígono buscado no tenga una construcción particular, ni pueda obtenerse como múltiplo de otro, dado que este procedimiento lleva inherente una gran imprecisión.

Comenzaremos con el trazado del diámetro A-B, que dividiremos, mediante el Teorema de Tales en tantas partes iguales como lados tenga el polígono que deseamos trazar. Para ello trazaremos desde B una recta r cualquiera, sobre la que llevaremos las divisiones iguales. Uniremos la última división, con A, y por el resto de divisiones trazaremos paralelas a esta, obteniendo de esta forma, la división de la diagonal A-B en partes iguales.

Con centro en A y B trazaremos dos arcos de radio A-B, los cuales se interceptarán en un punto F, desde el que trazaremos una semirecta que haremos pasar por la división 2 hasta cortar la circunferencia dando lugar a la división buscada. Solo restaría trasladar esta distancia o división como lado para obtener el polígono buscado.

TRAZADO DE POLÍGONOS REGULARES CONOCIENDO EL LADO

 -Procedimiento general-

Éste segundo método consiste en dibujar el hexágono regular del lado que te proporcionan y luego gracias al teorema de Tales obtienes los centros de las circunferencias que inscriben desde el heptágono al dodecágono (dividiendo el radio en 6 partes iguales). Si tiene más o menos lados, solo tienes que sumar o restar partes.

Control 2.4

 

Explicación de cómo se dibuja un corte..

 A continuación, el profesor Antonio Castilla nos explica cómo se dibuja un corte,  resolviendo como ejemplo un ejercicio de D.T. de Selectividad Andalucía (2014)

Ejercicio de determinación de un corte total:

enunciado

solución